이번 챕터에서는 알파고에 쓰인 강화 학습 알고리즘과 원리, 그에 더해 MCTS에 대해 배울 예정이다.
10.1 알파고
알파고를 이해할 때 학습 + 실시간 플래닝이라는 2단계로 나누어 접근하면 이해가 쉽다.
학습 단계: 알파고가 이세돌을 만나기 전에 이루어지는 과정
실시간 플래닝: 이세돌과 대국 도중 실시간으로 이루어지는 과정
알파고는 실시간 플래닝 알고리즘으로 MCTS를 사용한다.
학습단계
MCTS에서 쓰일 재료들을 만드는 단계이다.
MCTS는 크게 4가지 준비물을 필요로 한다.
1) 사람의 기보를 이용해 지도 학습한 정책 \(\pi_{sl}\)
2) 롤아웃 정책 \(\pi_{roll}\)
3) 스스로 대국하며 강화 학습한 정책 \(\pi_{rl}\)
4) 밸류 네트워크 \(v_{rl}\)

1) 지도 학습 정책 \(\pi_{sl}\)

- 알파고의 모든 과정은 바둑 기사의 기보 데이터를 활용해 \(\pi_{sl}\)이라는 뉴럴넷을 학습시키는 것으로부터 시작
- 바둑판의 상태 정보 가 인풋으로 들어오면 총 19*19 = 361개의 바둑 칸들 중 현재 둘 수 있는 곳에 대해 실제로 돌을 내려놓을 확률을 리턴 (361개의 클래스가 있고 그중에 하나로 분류(classification) 해주는 네트워크)
- 위와 같은 방법으로 3천만 개의 기보 안에 있는 "평균 전략"을 학습
- 13개 층의 컨볼루션 레이어(convolutional layer)를 쌓아 올려서 구성
- 바둑판의 정보를 토대로 사람의 지식을 이용하여 만든 feature를 48겹을 쌓아서 인풋으로 제공 (19×19×48)
- 학습 결과 \(\pi_{roll}\)은 주어진 데이터에 대해 57%의 정답률을 기록 (아마 5단 정도의 실력)
2) 롤아웃 정책 \(\pi_{roll}\)
- 롤아웃 정책 \(\pi_{roll}\)은 \(\pi_{roll}\)의 가벼운 버전
- 사람의 지식을 이용하여 만든 수많은 feature에 대해 선형 결합 레이어가 1개
- 속도가 매우 빠름
- 성능은 부족함
- 필요한 이유는 MCTS 단계에서 같은 시간 동안 더 많은 수를 시뮬레이션 해볼 수 있기 때문에
3) 스스로 대국하며 강화 학습한 정책 \(\pi_{rl}\)

- \(\pi_{rl}\)은 \(\pi_{sl}\)과 완벽히 똑같이 생긴 뉴럴 네트워크이고 \(\pi_{rl}\)의 파라미터들은 \(\pi_{sl}\)을 이용해 초기화
- \(\pi_{sl}\)로 초기화하는 것은 의미있는 경험을 배우고 학습하기에 고품질의 학습을 생산함
- \(\pi_{rl}\)은 self-play를 통해 계속해서 강화됨
- 자신의 과거 모델들을 이용해 풀을 만들고, 풀에서 랜덤하게 하나를 뽑아와서 경기를 펼침

- policy gradient 방법론을 사용하였고 그중에서도 리턴만 있으면 학습할 수 있는 REINFORCE 알고리즘 사용
- 값은 1.0 (진 경기는 -1, 이긴 경기는 +1)
- 학습이 끝난 \(\pi_{rl}\)은 80%의 승률로 \(\pi_{sl}\)을 이김
4) 밸류 네트워크 \(v_{rl}\)

- \(v_{rl}\)의 신경망 구조는과 동일하지만 아웃풋이 가 아니라 1개의 값
- 각 상태의 밸류를 리턴하는 네트워크이기 때문에
- 이고 중간 보상이 없기 때문에 결국 에서 시작하여 1을 받을지, -1을 받을지 예측하는 함수, 즉 승자를 예측하는 함수임
MCTS
MCTS는 주어진 상황에서 시작하여 "그냥 많이 둬 보는" 방법론
MCTS는 주어진 상황에 특화된 해를 찾는데 쓰이는 플래닝(planning) 알고리즘

- 주어진 상황을 라 하면 부터 시작하여 주어진 시간 안에 초대한 많은 게임을 시뮬레이션해 보는 것
- 에서 할 수 있는 액션 \(a_1\), \(a_2\), ..., \(a_{180}\)까지 할 수 있는 액션을 최대한 다양하게 해 봄
- 다양한 액션을 해 보고 결과가 가장 좋았던 액션을 실제로 선택하는 방법이 MCTS
MCTS 사용 조건
1) MDP의 모델을 알아야 함 \(P_{ss'}^a\), \(R_s^a\)
- 바둑의 규칙을 알고있다는 것이 모델을 안다는 뜻
- 이처럼 모델을 알 때, 이런 정보를 이용해 더 나은 정책을 만드는 과정을 플래닝이라고 한다
2) 게임 중간마다 시간적 틈이 있어야한다
- MCTS가 실행되는 시간
알파고에서의 MCTS 구성
- MCTS는 선택, 확장, 시뮬레이션, 백 프로파게이션 4 단계로 구성
- 4단계가 한 바퀴 돌면 새로운 노드가 생성됨, 노드(node)는 바둑판의 상태에 해당, 엣지(edge)는 액션에 해당
- 노드를 평가하고 그 노드에 오기까지 거쳐온 모든 경로의 모든 엣지(액션)의 가치를 업데이트
- 이 평가를 바탕으로 좋았던 액션을 선택
- 이 과정을 반복하면 새로운 노드가 매달리게 되고, 트리는 풍성해지며, 엣지의 가치, 즉 액션의 가치는 점점 더 정확해진다.
-
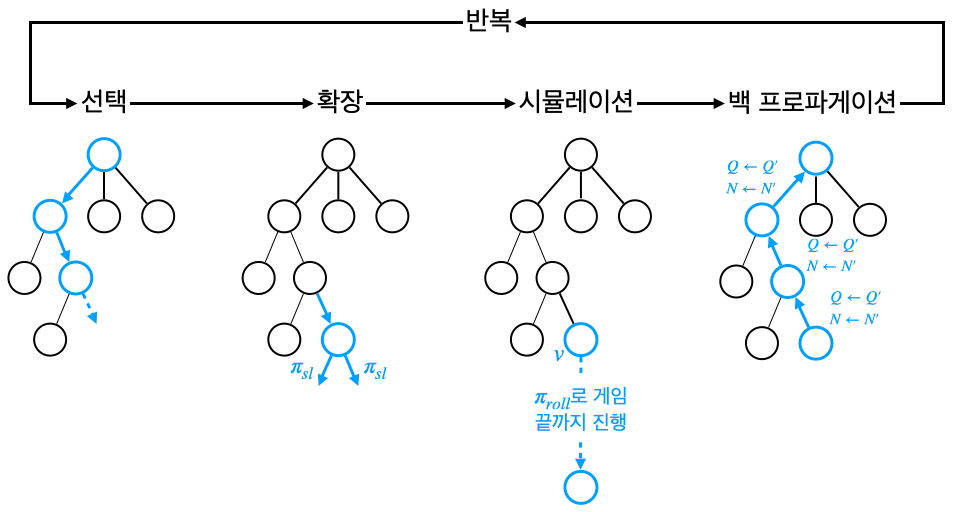
1) 선택
- 루트 노드에서 출발하여 리프 노드(leaf node, 자식이 없는 노드)까지 과는 과정
리프 노드에 도착하면 다음 단계인 확장 단계로 넘어감 - 기존에 평가해 놓은 각 액션의 벨류를 높은 액션을 선택
\(a_t = \underset{a}{\mathrm{argmax}} \left ( Q(s_t, a) + u(s_t, a) \right )\)
- \(Q(s_t,a)\) : 시뮬레이션 실행 후 얼마나 좋은지
- \(u(s_t, a)\) : 시뮬레이션 실행 전에 얼마나 좋을 것이라 추측하는지
- 경험이 쌓일수록 Q의 영향력은 커지고 u의 영향력은 줄어든다
Q(s,a)는 처음에는 0으로 초기화 > s에서 a를 실제로 선택한 경험이 발생하는 순간 Q(s,a)의 값이 조금씩 업데이트 > a를 선택한 이후 최종적으로 도달한 리프 노드의 밸류가 높으면 Q값 증가, 낮으면 Q값 감소
- 어떤 상태 \(s_{78}\)에서 액션 \(a_{33}\)을 선택하는 경험을 100번 했다고 가정
\(Q(s_{78}, a_{33}) = {1 \over 100} \sum_{i=1}^{100} V(s_L^i)\)
u(s,a)는 다음과 같음
- \(u(s_t, a) \propto {P(s, a) \over 1 + N(s, a)}\)
- 는 사전 확률(prior probability)로 시뮬레이션해 보기 전에 각 액션에 확률을 부여함. \(P(s, a) = \pi_{sl}(s, a)\)
- 는 시뮬레이션 도중 엣지 (s, a)를 지나간 횟수
- =0에서 시작하여 한 번 지나갈 때마다 1씩 더해 짐
시뮬레이션이 진행되면 분모가 커지면서 사전 확률의 영향이 줄어든다
\(\pi_{rl}\)대신 \(\pi_{sl}\)을 사전 확률로 사용한 이유는 \(\pi_{sl}\)이 더 다양한 액션을 시도하는 정책이었기 때문에 \(\pi_{sl}\)로 초기화 해주면, 그만큼 시뮬레이션 도중 다양한 수를 시도하여 다양한 경험을 쌓을 수 있다.
2) 확장
- 방금 도달한 리프 노드를 실제로 트리에 매달아 주는 과정
- 또한 이 노드에서 뻗어나가는 엣지들의 다양한 정보를 초기화
3) 시뮬레이션
- 리프 노드가 트리의 정식 노드가 되었기 때문에 노드의 가치를 평가, \(V(s_L)\)를 계산
- MCTS에서 노드의 벨류를 계산하는 두 가지 방법
- 리프 노드 \(s_L\)부터 시작하여 게임이 끝날 때까지 빠르게 시뮬레이션해 봄 ( \(\pi_{roll}\) 을 이용해 \(z_l\)계산 )
- 벨류 네트워크 \(v_{rl}\)(s) 를 활용
- 알파고는 위 두 가지 방법을 섞어서 계산
\(V(s_L) = {1 \over 2} v_{rl}(s_L) + {1 \over 2} z_L\)
4) 백프로파게이션
- 리프 노드 밸류의 평균값인 를 계산해 주는 과정
- 리프 노드에 도달하기까지 지나온 모든 엣지에 대해 Q(s,a)값과 N(s,a)값을 업데이트 해 준다.
\(\begin{equation} \begin{split} N(s, a) &\gets N(s, a) + 1 \\ Q(s, a) &\gets Q(s, a) + {1 \over N(s, a)} \left ( V(s_L) - Q(s, a) \right ) \\ \end{split} \end{equation}\)- 지나온 모든 엣지에 대해 카운터 값은 1증가, Q(s,a)값은 \(V(s_L)\)의 방향으로 조금 업데이트
- 밸류 값이 리프 노드로부터 루트 노드로 전파된 것이니 "역전파"라고 부름
이렇게 선택, 확장, 시뮬레이션, 백 프로파게이션 과정을 한 번 진행하면 하나의 노드가 새롭게 매달린다.
이를 이용해 액션을 선택하고자 하면 어떤 액션을 선택하는게 좋을까?
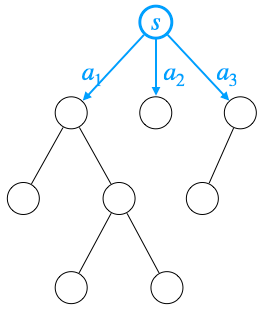
- MCTS에서 계산했던 액션 벨류인 가 가장 높은 액션이 제일 액션이라 할 수 있음
- 하지만 알파고는 대신 방문 횟수, 즉 가 가장 큰 액션을 선택, 위 그림에서는 \(a_1\)을 선택
아래 식과 같이 MCTS을 결정론적(deterministic)이 아닌 확률적(stochastic)으로도 움직일 수 있음
\(\pi_{mcts}(s, a_i) = {N(s, a_i) \over N(s, a_1) + N(s, a_2) + N(s, a_3)} \;\;\;\; i= 1, 2, 3\)
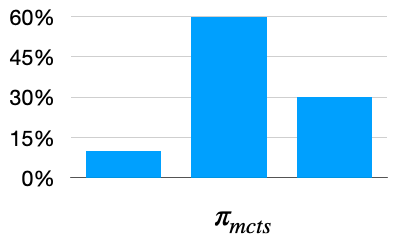
이 경우 MCTS를 마치고 난 뒤에도 루트 노드에서 실제로 선택하게 되는 액션은 매번 달라진다. MCTS의 결과가 정책 함수처럼 작동하는 것.
알파고 제로에서 \(\pi_{mcts}\)는 중요한 역할을 하게 된다.
10.2 알파고 제로
기보데이터의 도움 없이 학습이 가능한 방법이다.
기보데이터가 없기 때문에 강화 학습을 진행하게 되면, 완전한 랜덤 정책에서 시작할 것이다.
인간을 대신할 새로운 선생님, MCTS
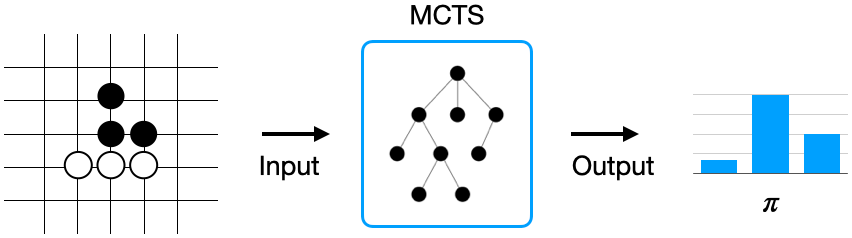
MCTS를 현재 상태 s를 인풋으로 받아서 그에 특화된 정책 \(\pi\)(s)를 내놓은 모듈로 생각해보자.
1) MCTS를 내부 상자로 감싸두면 이는 여러 번 시뮬레이션해 보고 얻은 결과 이기 때문에 현재 정책보다 좋은 정책일 것이다.
2) 이를 정답으로 보고 학습한다.
3) 스텝마다 MCTS를 돌려서 각 상황에 따른 정답 확률 분포를 얻고, 그 분포와 현재 정책 네트워크의 아웃풋 사이 차이를 줄이는 방향으로 정책 네트워크를 업데이트한다.
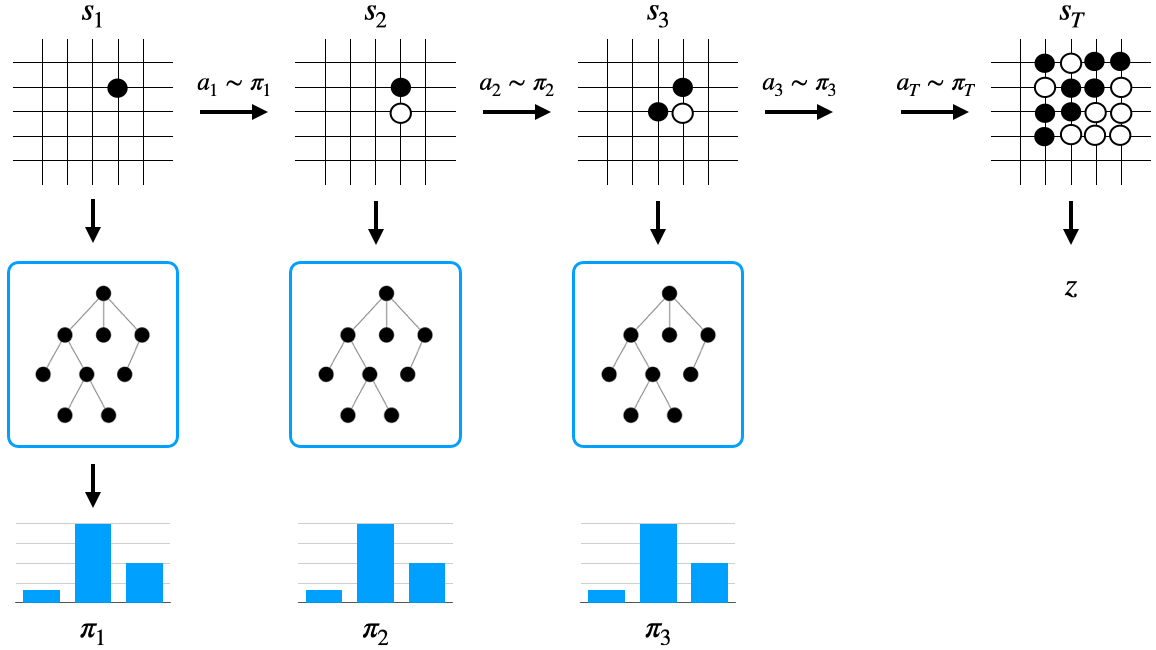
- 처음 상태 \(s_1\)에서 MCTS를 돌린다.
- 액션에 대한 확률 분포 \(\pi_1\)\((s_1)\)을 얻는다.
- 이 확률 분포에서 액션을 샘플링하여 \(a_1\)이 뽑혔다고 해보자.
- 그러면 \(a_1\)을 실행하고 상태 \(s_2\)에 도달한다.
- \(s_2\)에서도 MCTS를 돌린다.
- 액션에 대한 확률 분포 \(\pi_2\)\((s_2)\)을 얻는다.
- 이를 반복
각 데이터는 \((s_t, \pi_t, z_t)\) 형식, \(z_t\) 게임의 결과 (이겼으면 +1, 졌으면 -1)
이 데이터를 이용해 뉴럴넷 \(f_{\theta}\)를 학습
\(f_{\theta}(s) = (p, v)\)
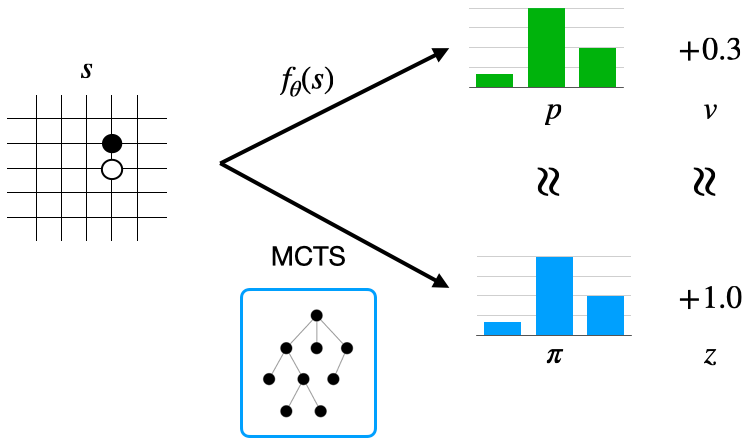
- 는 MCTS가 알려주는 확률 분포인 \(\pi_t\)와의 차이를 줄이는 방향으로 업데이트 (크로스 엔트로피)
- 는 경기 결괏값인 \(z_t\)와의 차이를 줄이는 방향으로 업데이트 (MSE)
알파고 제로에서의 MCTS
파파고에서 MCTS를 돌리기 위해 사람 데이터를 이용해 학습한 \(\pi_{sl}\)과 \(\pi_{roll}\), 그리고 강화 학습을 통해 얻은 \(v_{rl}\)이 필요했지만 이들은 더 이상 존재하지 않는다.
대신 학습되지 않은 뉴럴넷 \(f_{\theta}(s) = (p, v)\)이 존재한다. 이제 이 뉴럴넷을 사용해 MCTS를 진행한다.
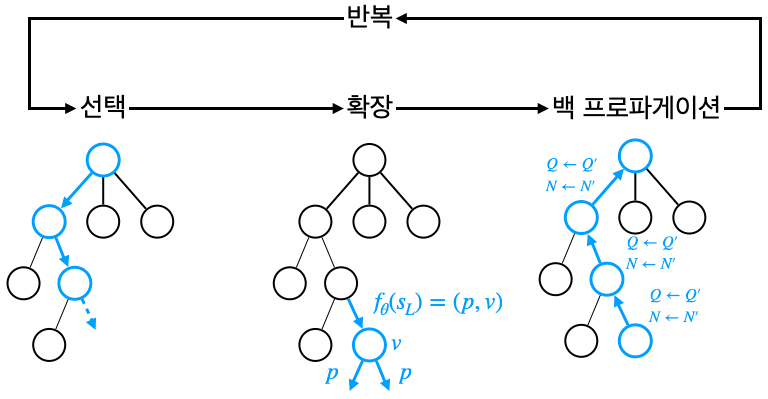
- 기존 확장 단계에서는 리프 노드 \(s_L\)에서 뻗어 나가는 액션의 사전 확률을 \(\pi_{sl}\)로 초기화했다.
- 이제는 \(\pi_{sl}\)이 없기 때문에 뉴럴넷의 아웃풋인 p를 이용해 초기화한다. (p는 초기에는 완전한 랜덤 정책)
- 학습이 진행됨에 따라 가 조금씩 발전할 것이기 때문에 MCTS 성능도 점점 좋아질 것으로 기대할 수 있다.
- 기존 평가 단계에서는 \(s_L\)의 밸류를 평가할 때 \(\pi_{roll}\)을 이용해 얻은 시뮬레이션 결과와 밸류 함수 아웃풋 v를 반반 섞어 사용했다.
- 이제는 \(\pi_{roll}\)이 없기 때문에 시뮬레이션 해볼 수 없다.
- 대신 \(s_L\)의 밸류를 평가할 때는 뉴럴넷의 아웃풋인 \(v\)를 사용한다.
뉴럴넷은 처음에는 랜덤으로 초기화되어 있다. 그러나 그럼에도 불구하고 MCTS를 돌린 결과가 기존 p보다 낫다. 랜덤 정책으로 바로 액션을 선택하는 것보다 랜덤 정책을 이용하여 MCTS를 해보고 그 중에서 결과가 좋았던 액션을 선택하는 것이 더 나은 정책이다.
'바닥부터 배우는 강화 학습' 카테고리의 다른 글
| 바닥부터 배우는 강화학습 1장부터 9장까지 총정리 (0) | 2024.01.15 |
|---|---|
| [ 바닥부터 배우는 강화 학습 ] 09. 정책 기반 에이전트 (2) | 2024.01.08 |
| [ 바닥부터 배우는 강화 학습 ] 08. 가치 기반 에이전트 (1) | 2024.01.08 |
| [ 바닥부터 배우는 강화 학습 ] 05. MDP를 모를 때 밸류 평가하기 (3) | 2024.01.02 |
| [ 바닥부터 배우는 강화 학습 ] 06. MDP를 모를 때 최고의 정책 찾기 (0) | 2023.11.23 |



