이번 챕터에서 다룰 문제는 어떠한 제약 조건도 더는 없는 상황이다.
첫 번째는 모델 프리 상황이고, 두 번째는 상태 공간과 액션 공간이 매우 커서 밸류를 일일이 테이블에 담지 못하는 상황에서의 해결책에 대해 다룰 예정이다.
큰 문제 공간을 다루기 위해 본격적으로 뉴럴넷과 강화학습이 접목한다.
강화 학습에 뉴럴넷을 접목시키는 접근법은 2가지이다.
1) 가치 함수 \(v_\pi\)(s)나 \(q_\pi\)(s,a)를 뉴럴넷으로 표현하는 방식
2) \(\pi\)(a|s) 자체를 뉴럴넷으로 표현하는 방식
더 자세한 설명을 하기 전에, 에이전트의 분류에 대해 살펴보자
가치 기반 에이전트는 가치 함수에 근거하여 액션을 선택 액션-가치 함수 q(s,a)의 값을 보고 액션을 선택
(챕터 6에서 설명한 것처럼 모델-프리 상황에서는 v(s)만 가지고 액션을 정할 수 없기 때문)
정책 기반 에이전트는 정책 함수 \(\pi\)(a|s)를 보고 직접 액션을 선택.
밸류를 보고 액션을 선택하지 않으며, 가치 함수를 따로 두지도 않는다.
\(\pi\)만 있으면 에이전트는 MDP 안에서 경험을 쌓을 수 있고 이 경험을 이용해 학습 과정에서 \(\pi\)를 강화한다.
강화 과정에서 가치 함수는 쓰이지 않는다.
액터-크리틱은 가치 함수와 정책 함수 모두 사용한다.
액터 = 정책 \(\pi\), 크리틱 = 가치 함수 v(s) 또는 q(s,a)
챕터 9에서 다뤄보자
8.1 밸류 네트워크의 학습
그림과 같이 뉴럴넷으로 이루어진 가치 함수가 있다고 해보자. 이 뉴럴넷을 밸류 네트워크라고 부른다.
길이가 2인 벡터 인풋 s를 받아서 특정 정책 \(\pi\)를 따랐을 때의 밸류를 리턴하는 뉴럴넷이다.
\(v_\theta\)(s) 여기서 \(\theta\)는 뉴럴넷의 파라미터이고 처음에는 랜덤으로 초기화되어 있다.
목표는 적절한 \(\theta\)를 학습하여 \(v_\theta\)(s)가 각 상태별로 올바른 밸류를 출력하도록 하는 것이다.
뉴럴넷을 학습하려면 결국 예측과 정답 사이 차이를 뜻하는 손실 함수를 정의해야 한다. 이를 위해서는 정답이 필요하지만 우리는 이를 알지 못한다.
일단 상태별 밸류의 값을 \(v_{true}(s)\)라고 가정한다.
그러면 손실 함수는 L\((\theta)\)=\((v_{true}(s) - v_{\theta}(s))^2\) 이다.
이것이 엄밀한 정의가 아닌 이유는ㅍ어떤 s에 대해 위 값을 계산할 것인지가 빠졌기 때문이다.
이를 위해 \(L(\theta)=\mathbb{E} \left [ (v_{true}(s) - v_{\theta}(s))^2 \right ]\) 해당 정의를 선택한다.
\(L(\theta)\)의 \(\theta\)에 대한 그라디언트를 계산해보자.
\(\nabla_{\theta} L(\theta)=- \mathbb{E} \left [ (v_{true}(s) - v_{\theta}(s)) \nabla_{\theta} v_{\theta}(s) \right ]\)
샘플을 1개만 뽑아보자 챕터 7에서 배웠던 식을 가져온다. 파라미터를 가리키는 변수가 w에서 \(\theta\)로만 바뀌었을 뿐 같은 식이다.
\(\begin{equation} \begin{split} \theta' &= \theta - \alpha \nabla_{\theta}L(\theta) \\ &= \theta + \alpha (v_{true}(s) - v_{\theta}(s)) \nabla_{\theta}v_{\theta}(s) \end{split} \end{equation}\)
이렇게 데이터 1개에 대해 \(\theta\)의 업데이트가 끝났고 이 과정을 샘플 1억 개에 대해 1억 번 반복하면 \(v_\theta\)(s)는 \(v_{true}\)(s)와 거의 같아진다.
하지만 실제 상황에서 실제 가치 함수인 \(v_{true}\)(s)가 주어질 일이 없다. 하지만 챕터 5를 공부했으니 그를 대신하는 선택지를 알고 있다.
1) 몬테카를로 리턴
시점 t에서 시작해 에피소드가 끝날 때까지 얻은 감쇠된 누적 보상을 리턴 \(G_t\)로 표현했다.
\(V(s_t) \gets V(s_t) + \alpha(G_t - V(s_t))\)
위 식은 테이블 업데이트에 쓰였던 식이고 뉴럴넷을 업데이트하려면 결국 손실 함수를 정의해야 한다.
손실 함수의 정답 \(v_true\)(s) 자리에 \(G_t\)를 대입한다.
\(L(\theta)=\mathbb{E} \left [ (G_t - v_{\theta}(s))^2 \right ]\)
손실 함수 \(L_\theta\)가 정의되고 나면 \(\theta\)를 업데이트하는 방식은 동일하므로 생략하고 결과를 적어보자.
\(\theta' = \theta + \alpha (G_t - v_{\theta}(s)) \nabla_{\theta}v_{\theta}(s)\)
이를 이용해 \(\theta\)를 계속해서 업데이트해 나가면 점점 손실 함수의 값이 줄어들고 뉴럴넷의 아웃풋이 실제 밸류에 수렴한다.
2) TD타깃
TD 학습 방법은 한 스텝 더 진행해서 추측한 값을 이용해 현재의 추측치를 업데이트하는 방식이다.
그래서 이전 정답지에 리턴 \(G_t\)가 들어갔던 반면 이번에는 TD 타깃인 \(r_{t+1} + \gamma v_{\theta}(s_{t+1})\)를 대입한다. 손실 함수는 다음과 같다.
\(L(\theta)=\mathbb{E}_\pi \left [ (r_{t+1} + \gamma v_{\theta}(s_{t+1}) - v_{\theta}(s))^2 \right ]\)
이로부터 유도되는 파라미터 업데이트 식이다.
\(\theta' = \theta + \alpha (r_{t+1} + \gamma v_{\theta}(s_{t+1}) - v_{\theta}(s)) \nabla_{\theta}v_{\theta}(s)\)
+) \(v_{\theta}(s_{t+1})\)은 반드시 상수로 취급해야 한다.
8.2 딥 Q러닝
가치 기반 에이전트는 명시적 정책이 따로 없다. 즉 \(\pi\)없이 액션-가치 함수 q(s,a)를 이용한다.
q(s,a)는 각 상태 s에서 액션별 가치를 나타낸다. 따라서 각 상태에서 가장 가치가 높은 액션을 선택하는 식으로 정책을 만들 수 있다.
가치 함수는 밸류만 평가하는 함수인데 이를 마치 정책 함수처럼 사용하는 것이다. 이런 경우의 정책 함수를 내재된 정책이라고 한다.
이번에 배울 딥 Q러닝은 q(s,a)를 내재된 정책으로 사용한다. 챕터 6에서 배운 내용과 같으나 테이블 기반 방법론이 아닌 뉴럴넷을 이용하여 q(s,a)를 표현한다.
이론적 배경 - Q러닝
Q러닝을 복습해보자면 Q러닝은 결국 벨만 최적 방정식을 이용해 \(Q_*\)(s,a)를 학습하는 내용이었다.
벨만 최적 방정식과 이를 이용한 테이블 업데이트 수식을 적어보자.
\(\begin{equation} \begin{split} Q_*(s, a) &= \mathbb{E}_{s'} \left [ r + \gamma \underset{a'}{\mathrm{max}}Q_*(s', a') \right ] \\ Q(s, a) \gets Q(s, a) &+ \alpha (r + \gamma \underset{a'}{\mathrm{max}}Q(s', a') - Q(s, a)) \end{split} \end{equation}\)
딥 Q러닝은 여기까지의 내용을 뉴럴넷으로 확장하기만 하면 된다.뉴럴넷을 이용해 Q(s,a) 함수를 표현하기 때문에 \(Q_\theta\)(s,a)라고 표기하자. (\(\theta\)는 뉴럴넷의 파라미터 벡터)
- 테이블의 업데이트 식을 보면 정답인 r + \(\gamma \underset{a'}{\mathrm{max}}\)\(Q_{*}\)(s', a')와 현재 추측치인 Q(s,a) 사이 차이를 줄이는 방향으로 업데이트
- 뉴럴넷은 r + \(\gamma \underset{a'}{\mathrm{max}}\)Q(s', a') 를 정답이라고 보고 이것과 \(Q_\theta\)(s,a) 사이 차이의 제곱을 손실함수로 정의
\(L(\theta) = \mathbb{E} \left [ (r + \gamma \underset{a'}{\mathrm{max}} Q_{\theta}(s', a') - Q_{\theta}(s, a))^2 \right ]\)
데이터를 모아 평균으로 업데이트했었다. 이런 방식으로 하나의 데이터에 대해 \(\theta\)를 업데이트 하는 식을 적어보자
\(\theta' = \theta + \alpha \left ( r + \gamma \underset{a'}{\mathrm{max}} Q_{\theta}(s', a') - Q_{\theta}(s, a) \right ) \nabla_{\theta}Q_{\theta}(s, a)\)
이 식을 이용해 \(\theta\)를 업데이트하면 \(Q_\theta\)(s,a)는 점점 최적의 액션-가치 함수 \(Q_*\)(s,a)에 가까워질 것이다.
기댓값 연산자를 없애기 위해 여러 개의 샘플을 뽑아서 평균을 이용해 업데이트함. 이처럼 복수의 데이터를 모아 놓은 것을 미니 배치(mini-batch)라 함
딥 Q러닝 pseudo code
+) Q러닝이 off-policy 임을 볼 수 있음
익스피리언스 리플레이와 타깃 네트워크
DQN의 본질은 뉴럴넷으로 Q함수를 강화하는 것
이를 위한 방법 2가지를 알아보자
1) 익스피리언스 리플레이(Experience Replay)
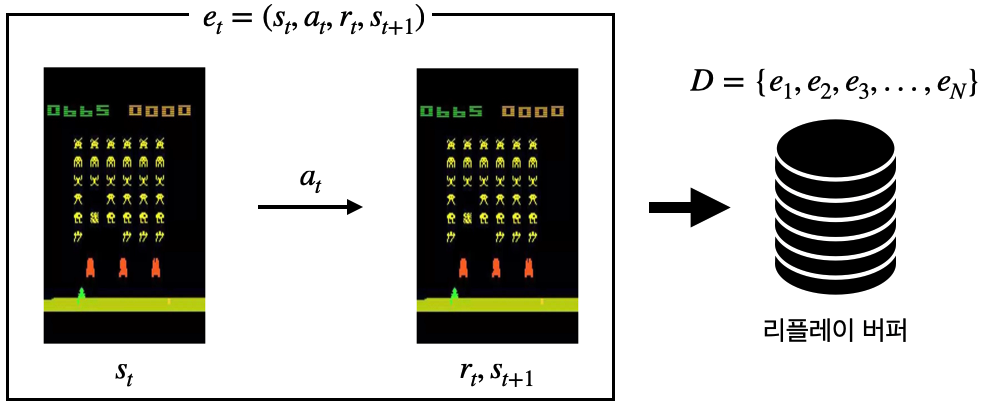
- "겪었던 경험을 재사용하면 더 좋지 않을까?" 하는 아이디어에서 출발
- 하나의 상태 전이(transition) \(e_t\)는 \(s_t\),\(a_t\),\(r_t\),\(s_{t+1}\)로 표현 가능
상태 에서 액션 를 했더니 보상 을 받고 다음 상태\(s_{t+1}\)에 도착하였다"는 뜻
리플레이 버퍼
- 가장 최근에 발생한 데이터 n개를 버퍼에 저장
- 새로운 데이터가 하나 버퍼에 들어오면 가장 오래된 데이터를 하나 제거
- 학습할 때는 버퍼에서 임의로 데이터를 뽑아서 사용. (예, 32개씩 미니 배치 단위로 학습)
- 각각의 데이터 사이 상관성(correalation)이 작아서 더 효율적으로 학습 가능
- off-policy 알고리즘에만 사용할 수 있음
2) 별도의 타깃 네트워크
손실함수의 \(L(\theta)\)의 의미는 정답과 추측 사이의 차이이며 이 차이를 줄이는 방향으로 \(\theta\)가 업데이트 된다.
그런데 Q러닝에서는 \(R + \gamma \underset{A'}{\mathrm{max}} Q_{\theta_i} (S', A') \)이 정답으로 사용되기 때문에 정답이 \(\theta\)에 의존적이다. 이는 정답에 해당하는 값이 계속해서 변하므로 안정적인 학습에 해가 된다.
\(R + \gamma \underset{A'}{\mathrm{max}} Q_{\theta_i} (S', A') \to R + \gamma \underset{A'}{\mathrm{max}} Q_{\theta_{i+1}} (S', A')\)
그래서 타깃 네트워크란
- 정답을 계산할 때 사용하는 타깃 네트워크와 학습을 받고 있는 Q 네트워크 두 벌의 네트워크 준비
- 정답을 계산할 때 사용하는 네트워크의 파라미터를 잠시 얼려둔다.
- 그 사이 학습을 받고 있는 네트워크의 파라미터는 계속해서 업데이트 된다.
DQN 구현
# 라이브러리 import
import gym # OpenAI GYM 라이브러리
import collections # deque 활용
import random
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
# 하이퍼 파라미터 정의
learning_rate = 0.0005
gamma = 0.98
buffer_limit = 50000
batch_size = 32
# 리플레이 버퍼 클래스
class ReplayBuffer():
def __init__(self):
self.buffer = collections.deque(maxlen=buffer_limit)
def put(self, transition):
self.buffer.append(transition)
def sample(self, n):
mini_batch = random.sample(self.buffer, n)
s_lst, a_lst, r_lst, s_prime_lst, done_mask_lst = [], [], [], [], []
# done_mask_lst : 종료 상태의 밸류를 마스킹해주기 위해 만든 변수
for transition in mini_batch:
s, a, r, s_prime, done_mask = transition
s_lst.append(s)
a_lst.append([a])
r_lst.append([r])
s_prime_lst.append(s_prime)
done_mask_lst.append([done_mask])
return torch.tensor(s_lst, dtype=torch.float), torch.tensor(a_lst), torch.tensor(r_lst), \
torch.tensor(s_prime_lst, dtype=torch.float), torch.tensor(done_mask_lst)
def size(self):
return len(self.buffer)
# Q밸류 네트워크 클래스
class Qnet(nn.Module):
'''
nn.Module 클래스는 파이토치 라이브러리 안에 포함된 클래스로,
뉴럴넷을 만들 때 뼈대가 되는 클래스이며 뉴럴넷과 관련한 다양한 연산을
제공해주기 때문에 파이토치에서 뉴럴넷을 선언할 때 거의 디폴트로 상속받는 클래스
'''
def __init__(self):
super(Qnet, self).__init__()
self.fc1 = nn.Linear(4, 128)
self.fc2 = nn.Linear(128, 128)
self.fc3 = nn.Linear(128, 2)
def forward(self, x):
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
x = self.fc3(x)
return x
def sample_action(self, obs, epsilon):
out = self.forward(obs)
coin = random.random()
if coin < epsilon:
return random.randint(0, 1)
else:
return out.argmax().item()
# 학습 함수
def train(q, q_target, memory, optimizer):
for i in range(10):
s,a,r,s_prime,done_mask = memory.sample(batch_size)
q_out = q(s)
q_a = q_out.gather(1,a)
max_q_prime = q_target(s_prime).max(1)[0].unsqueeze(1)
target = r + gamma*max_q_prime*done_mask
loss = F.smooth_l1_loss(q_a, target)
optimizer.zero_grad()
loss.backward() # loss에 대한 그라디언트 계산이 일어남
optimizer.step()
# 메인 함수
def main():
env = gym.make('CartPole-v1')
q = Qnet()
q_target = Qnet()
q_target.load_state_dict(q.state_dict())
memory = ReplayBuffer()
print_interval = 20
score = 0.0
optimizer = optim.Adam(q.parameters(), lr = learning_rate)
for n_epi in range(10000):
epsilon = max(0.01, 0.08 - 0.01*(n_epi/200))
# Linear annealing from 8% to 1%
s = env.reset()
done = False
while not done:
a = q.sample_action(torch.from_numpy(s).float(), epsilon)
s_prime, r, done, info = env.step(a)
done_mask = 0.0 if done else 1.0
memory.put((s,a,r/100.0,s_prime,done_mask))
s = s_prime
score += r
if done:
break
if memory.size()>2000:
train(q, q_target, memory, optimizer)
if n_epi%print_interval==0 and n_epi!=0:
q_target.load_state_dict(q.state_dict())
print("n_episode : {}, score : {:.1f}, n_buffer : {}, eps : {:.1f}%".format(n_epi, score/print_interval, memory.size(), epsilon*100))
score = 0.0
env.close()'바닥부터 배우는 강화 학습' 카테고리의 다른 글
| [ 바닥부터 배우는 강화 학습 ] 10. 알파고와 MCTS (1) | 2024.01.09 |
|---|---|
| [ 바닥부터 배우는 강화 학습 ] 09. 정책 기반 에이전트 (2) | 2024.01.08 |
| [ 바닥부터 배우는 강화 학습 ] 05. MDP를 모를 때 밸류 평가하기 (3) | 2024.01.02 |
| [ 바닥부터 배우는 강화 학습 ] 06. MDP를 모를 때 최고의 정책 찾기 (0) | 2023.11.23 |
| [ 바닥부터 배우는 강화 학습 ] 04. MDP를 알 때의 플래닝 (0) | 2023.11.10 |
