이전 챕터에서 Prediction 문제를 풀었다면 이번 챕터에서는 Control 문제를 해결할 차례이다.
밸류를 계산할 수 있기 때문에 이를 이용해 정책을 찾는 것은 한결 쉽다. Q러닝도 이번 챕터에서 등장한다.
우리는 이제 주어진 정책을 평가하는 방법론인 MC와 TD를 알고있다.
이 방법론을 통해 어떠한 정책이 주어져도, MDP에 대한 정보를 몰라도 각 상태의 가치를 평가할 수 있게 되었다.
해당 정책을 따라서 에이전트가 움직이게 한 다음에 에이전트가 쌓은 경험으로부터 각 상태의 가치를 학습하는 방식이었다.
그러나 이는 주어진 정책을 평가하는 방법론일 뿐 최고의 정책을 찾는 방법에 대해 살펴보자.
여전히 상태 개수나 액션 개수가 적은 MDP 세팅이어야하며, MDP에 대한 정보를 모르고 있어야 한다.
이러한 상황에서 control 방법 중 가장 대표적인 3가지 방법론(몬테카를로 컨트롤, SARSA, Q러닝)을 배워보자.
6.1 몬테카를로 컨트롤
4장에서 배웠던 정책 이터레이션 : 임의의 정책에서 시작해 정책을 평가하여 밸류를 계산하고, 계산한 밸류에 대해 그리디 정책을 만드는 과정을 계속해 반복하는 방법
챕터 4로부터 달라진 것은 모델-프리로 바뀌었다는 부분이다. 모델-프리에서 정책 이터레이션을 그대로 사용할 수 없을까?
정책 이터레이션을 그대로 사용할 수 없는 이유
평가 단계에서는 반복적 정책 평가를, 개선 단계에서는 그리디 정책 생성을 이용했다.
이를 그대로 적용할 수 없는 두가지 문제가 있다.
1) 평가 단계에서 반복적 정책 평가를 사용할 수 없다.
반복적 정책 평가의 핵심이 되었던 벨만 기대 방정식 2단계를 살펴보자.
\(v_{\pi}(s) = \sum_{a \in A} \pi(a|s) \left( r_s^a + \gamma \sum_{s' \in S} P_{ss'}^a v_{\pi}(s') \right)\)
\(r_s^a\)와 \(p_{ss'}^a\)는 MDP에 대한 정보를 알아야만 채울 수 있는 값이다.
즉 어떤 액션을 했을 때 보상이 어떻게 될지, 다음 상태의 확률 분포가 어떻게 될지를 미리 알고 있어야 벨만 기대 방정식을 통해 현재 상태의 가치를 업데이트할 수 있다.
그러나 모델프리 상황에서는 보상을 알려면 직접 액션을 해서 값을 받아야하며 다음 상태가 어디가 될지도 실제로 액션을 해서 어디 도착하는지 봐야만 알 수 있다. 또한 얼마의 확률로 이 상태에 도착했는지, 다른 상태에 도착할 확률을 얼마인지 등에 대해서는 알 수 없다.
2) 정책 개선 단계에서 그리디 정책을 만들 수 없다.
예를 들어 \(s_1\)의 밸류는 1이고, \(s_2\)의 밸류는 2이다. MDP의 모든 정보를 안다면 현재 상태 \(s_0\)에서 \(a_1\)을 선택하면 \(s_1\)에 도착하며, \(a_2\)를 선택하면 \(s_2\)에 도착한다는 것을 알 수 있다.
즉 \(s_0\)에서의 그리디 정책은 \(\pi_{greedy}(s_0) = a_2\)이다.
하지만 MDP의 상태 전이에 대한 정보를 모른다면 현재 상태에서 각 액션을 선택했을 때 다음 상태가 어디가 될지 알 수 없다. (\(a_1\)이나 \(a_2\)를 선택했을 때 어떤 상태에 도착할 지 알 수 없음) 이런 상황에서는 더 나은 액션을 선택할 수 없다. 액션을 선택하면 도달하게 되는 상태의 밸류를 통해 액션의 우열을 판단했으나 이제는 어떤 상태에 도달할지 알 수 없기에 도착하는 상태의 밸류 또한 비교할 수 없다.
해결 방법
1) 평가 자리에 MC
첫 번째 문제는 반복적 정책 평가가 불가능하다는 점이었다. 하지만 챕터 5에서 MDP를 모를 때 밸류를 계산하는 2가지 방법론을 배웠다. 그 중 하나를 정책 평가 단계에 넣으면 된다.
MC를 평가 단계에서 사용하면 벨만 기대 방정식 2단계 수식들을 사용하지 않아도 각 상태의 밸류를 평가할 수 있게 된다.
2) V 대신 Q
두 번째 문제는 상태 가치 함수인 v(s)만 가지고는 정책 개선 단계에서 그리디 정책을 생성할 수 없다는 점이었다.
그래서 v(s) 대신에 상태-액션 가치 함수인 q(s,a)를 이용한다.
상태-액션 가치 함수인 q(s,a)를 알면 그리디 액션을 선택할 수 있다.
상태 s에서 각 액션을 선택하면 어느 상태로 도달하는지는 모르지만 각 액션을 선택하는 것의 밸류는 알겠으니, 밸류가 제일 높은 액션을 선택한다.
즉 몬테카를로 방법을 이용해 q(s,a)를 구하는 것이 핵심이다. 그 외에는 정책 이터레이션의 방법론을 그대로 따르는 것이다.
MC를 이용해 q(s,a) 함수를 계산하고 평가된 q(s,a)를 이용해 새로운 그리디 정책을 만들고 이 정책에 다시 MC를 이용해 q(s,a)를 계산하고 반복한다. 그리고 마지막 단계에서 탐색을 진행한다.
우린 개선 단계에서 그리디 정책을 사용해왔다.
만약 모든 값이 0으로 초기화되었을 때 한 액션의 값이 업데이트되고 나머지는 모두 0일 때, 그 한 액션의 값이 한 번 치고 나가는 순간 큰일이 날 수 있다. 그래서 항상 액션을 그리디하게 선택해서는 안되며 에이전트의 탐색을 보장해주어야한다. 그러기 위해서는 탐색의 정도가 필요하다. 여기선 입실론 그리디를 소개한다.
3) greedy 대신 ε-greedy
ε이라는 작은 확률만큼 랜덤하게 선택하고 1-ε라는 나머지 확률은 원래처럼 그리디 액션을 선택한다. 좋은 방법은 ε의 값을 처음에는 높게 하다가 점점 줄여주는 것이다. 이런 방법론은 decaying ε-greedy라고 부른다.
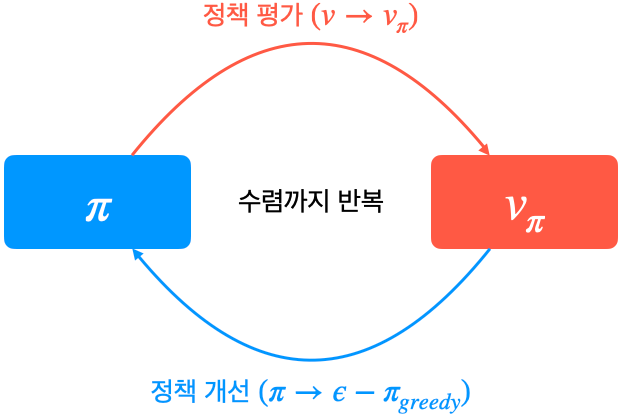
몬테카를로 컨트롤 구현
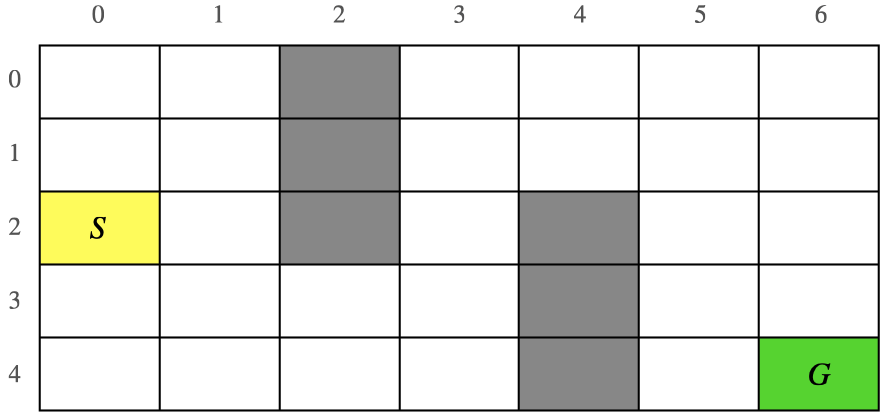
1) S에서 출발해 G에 도착하면 끝
2) 회색 영역은 지나갈 수 없음
3) 보상은 스텝마다 -1 (즉 최단거리로 도착하는 것이 가장 좋음)
해결방법
- 수렴할 때까지 n번 반복
--> 한 에피소드의 경험을 쌓고
--> 경험한 데이터로 q(s,a) 테이블의 값을 업데이트하고 (정책 평가)
--> 업데이트된 q(s,a) 테이블을 이용해 ε-greedy 정책을 만들고 (정책 개선)
실제 구현으로 넘어가보자
# GridWordl 클래스
class GridWorld():
'''
환경에 대한 함수 클래스
'''
def __init__(self):
self.x=0
self.y=0
def step(self, a):
# 0번 액션: 왼쪽, 1번 액션: 위, 2번 액션: 오른쪽, 3번 액션: 아래쪽
if a==0:
self.move_left()
elif a==1:
self.move_up()
elif a==2:
self.move_right()
elif a==3:
self.move_down()
reward = -1 # 보상은 항상 -1로 고정
done = self.is_done()
return (self.x, self.y), reward, done
def move_left(self):
if self.y==0:
pass
elif self.y==3 and self.x in [0,1,2]:
pass
elif self.y==5 and self.x in [2,3,4]:
pass
else:
self.y -= 1
def move_right(self):
if self.y==1 and self.x in [0,1,2]:
pass
elif self.y==3 and self.x in [2,3,4]:
pass
elif self.y==6:
pass
else:
self.y += 1
def move_up(self):
if self.x==0:
pass
elif self.x==3 and self.y==2:
pass
else:
self.x -= 1
def move_down(self):
if self.x==4:
pass
elif self.x==1 and self.y==4:
pass
else:
self.x+=1
def is_done(self):
if self.x==4 and self.y==6: # 목표 지점인 (4,6)에 도달하면 끝난다
return True
else:
return False
def reset(self):
self.x = 0
self.y = 0
return (self.x, self.y)
가장 중요한 함수는 step함수
- 에이전트로부터 액션을 받아서 다음 상태와 보상, 에피소드가 끝났는지 여부를 리턴
# QAgent 클래스
class QAgent():
def __init__(self):
self.q_table = np.zeros((5,7,4)) # q밸류를 저장하는 변수, 모두 0으로 초기화
self.eps = 0.9 # 입실론 설정
self.alpha = 0.01
def select_action(self, s):
# eps-greedy로 액션을 선택
x, y = s
coin = random.random()
if coin < self.eps:
action = random.randint(0,3)
else:
action_val = self.q_table[x,y,:]
action = np.argmax(action_val)
return action
def update_table(self, history):
# 한 에피소드에 해당하는 history를 입력으로 받아 q 테이블의 값을 업데이트 한다.
cum_reward = 0
for transition in history[::-1]:
s, a, r, s_prime = transition
x, y = s
# 몬테카를로 방식을 이용하여 업데이트
self.q_table[x,y,a] = self.q_table[x,y,a] + self.alpha * (cum_reward - self.q_table[x,y,a])
cum_reward = cum_reward + r
def anneal_eps(self):
self.eps -= 0.03
self.eps = max(self.eps, 0.1)
def show_table(self):
# 학습이 각 위치에서 어느 액션의 q 값이 가장 높았는지 보여주는 함수
q_lst = self.q_table.tolist()
data = np.zeros((5,7))
for row_idx in range(len(q_lst)):
row = q_lst[row_idx]
for col_idx in range(len(row)):
col = row[col_idx]
action = np.argmax(col)
data[row_idx, col_idx] = action
print(data)
selection_action함수를 통해 s를 인풋으로 받아 s에서 알맞은 액션을 ε-greedy로 선택
# 메인 함수
def main():
env = GridWorld()
agent = QAgent()
for n_epi in range(1000) : # 총 n 에피소드 동안 학습
done = False
history = []
s = env.reset()
while not done: # 한 에피소드가 끝날 때 까지
a = agent.select_action(s)
s_prime, r, done = env.step(a)
history.append((s, a, r, s_prime))
s = s_prime
agent.update_table(history) # 히스토리를 이용하여 에이전트를 업데이트
agent.anneal_eps()
agent.show_table()
위 결과는 ε-greedy라는 확률적 요소가 액션을 선택하는 과정에 들어가 있기에 에피소드마다 방문하는 상태가 달라진다.
6.2 TD 컨트롤 1 - SARSA
평가단계에서 MC를 사용하는 것이 MC 컨트롤이었다.
MC 대신 TD를 사용하면 안될까?
가능하다.
MC 대신 TD
MC 대신 TD를 이용해 q(s,a)를 구해보자. TD를 이용해 Q를 계산하는 접근법을 가리키는 이름은 SARSA이다.
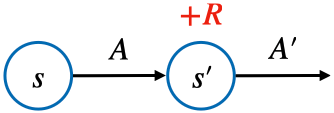
s에서 a를 선택하면 r을 받고 상태 s'에 도착하고 상태 s'에서는 다음 액션 a'을 선택한다. 이것을 이어적으면 SARSA가 된다.
TD로 V 학습 : \(V(S) \gets V(S) + \alpha (R + \gamma V(S') - V(S))\)
TD로 Q 학습 (SARSA) : \(Q(S, A) \gets Q(S, A) + \alpha (R + \gamma Q(S', A') - Q(S, A))\)
벨만 기대 방정식 0단계
TD로 V 학습 : \(v_{\pi}(s_t) = \mathbb{E} [r_{t+1} + \gamma v_{\pi}(s_{t+1})]\)
TD로 Q 학습 (SARSA) : \(q_{\pi}(s_t, a_t) = \mathbb{E} [r_{t+1} + \gamma q_{\pi}(s_{t+1}, a_{t+1})]\)
TD 타깃에 해당하는 식이 모두 벨만 기대 방정식으로부터 나온 것임을 알 수 있다.
기댓값 안의 샘플을 무수히 모으면 결국 실제 가치와 가까워질 것이기에 에이전트를 환경에 던져 놓고, 에이전트가 자신의 정책 함수 \(\pi\)를 이용해 자유롭게 거닐게 하다가 한 스텝의 데이터가 생성될 때마다 이 데이터를 통해 TD 타깃을 계산하여 기존의 테이블에 있던 값들을 조금씩 업데이트해 나가는 방식이다.
SARSA 구현
# QAgent 클래스
class QAgent():
def __init__(self):
self.q_table = np.zeros((5,7,4)) # 마찬가지로 Q테이블을 모두 0으로 초기화
self.eps = 0.9 # 입실론 설정
def select_action(self, s):
x, y = s
coin = random.random()
if coin < self.eps:
action = random.randint(0,3)
else:
action_val = self.q_table[x,y,:]
action = np.argmax(action_val)
return action
def update_table(self, transition):
s, a, r, s_prime = transition
x, y = s
next_x, next_y = s_prime
a_prime = self.select_action(s_prime) # s'에서 선택할 액션(실제로 취한 액션이 아님)
# SARSA 엡데이트 식을 이용
self.q_table[x,y,a] = self.q_table[x,y,a] + 0.1 * (r + self.q_table[next_x, next_y, a_prime] - self.q_table[x,y,a])
def anneal_eps(self):
self.eps -= 0.03
self.eps = max(self.eps, 0.1)
def show_table(self):
q_lst = self.q_table.tolist()
data = np.zeros((5,7))
for row_idx in range(len(q_lst)):
row = q_lst[row_idx]
for col_idx in range(len(row)):
col = row[col_idx]
action = np.argmax(col)
data[row_idx, col_idx] = action
print(data)
update_table 함수가 바뀌었다. MC에서는 update_table 함수가 에이전트가 경험한 history 전체를 인자로 받았으나 이제는 트랜지션을 인풋으로 받는다. (트렌지션 = 상태 전이 1번 한 것, s에서 a를 해서 r을 받고 s'에 도달한 것)
6.3 TD 컨트롤 2 - Q러닝
SARSA와 마찬가지로 TD를 이용해 최적의 정책을 찾는 방법이다.
SARSA와 Q러닝 모두 TD를 이용한 컨트롤 방법론인데 그 차이는 무엇일까?
SARSA는 on-policy이고, Q러닝은 off-policy인 것이다.
이를 위해 off-policy와 on-policy를 이해해야 한다.
off-policy와 on-policy
on-policy : 타깃 정책과 행동 정책이 같은 경우
off-policy : 타깃 정책과 행동 정책이 다른경우
타깃 정책? = 강화하고자 하는 목표가 되는 정책
행동 정책? = 환경과 상호 작용하며 경험을 쌓고 있는 정책
off-policy 는 결과가 좋았던 것은 그대로 따라하기도 하지만, 결과가 좋지 않았던 것은 수정하기도 한다.
지도학습은 그대로 따라하는 방식으로 학습된다. 그러나 off-policy는 강화 학습에 해당하며 무조건 따라하도록 학습하지 않는다.
off-policy의 장점
1) 과거의 경험을 재사용할 수 있다.
\(\pi_0\)를 업데이트 하기 위해 경험 100개를 쌓았고 이를 바탕으로 \(\pi_0\)을 \(\pi_1\)로 업데이트 했다.
여기서 on-policy 방법으로 다시 \(\pi_1\)을 학습하려면 \(\pi_1\)을 이용해 경험을 다시 처음부터 쌓아야 한다.
on-policy 방법론은 반드시 행동 정책과 타깃 정택이 동일하기 때문이다.
하지만 off-policy 방법론은 타깃 정책과 행동 정책이 달라도 되기에 \(\pi_0\)가 경험한 샘플들을 \(\pi_1\)의 업데이트에 그대로 재사용할 수 있다.
2) 사람의 데이터로부터 학습할 수 있다.
바둑을 플레이하는 에이전트를 학습시킨다고 할 때에 프로 바둑 기사가 뒀던 기보를 활용할 수 있다.
(s,a,r,s')로 이루어진 데이터만 있다면 학습에 쓸 수 있기 때문.
3) 일대다, 다대일 학습이 가능하다.
동시에 여러개의 정책을 학습시킬 수 있고 반대로 동시에 여러 개의 정책이 겪은 데이터를 모아 단 1개의 정책을 업데이트 할 수 있다.
행동 정책과 타깃 정책이 달라도 되기 때문이다.
Q러닝의 이론적 배경 - 벨만 최적 방정식
벨만 최적 방정식은 최적의 액션 밸류 \(q_{*}(s,a)\)에 대한 식으로 존재하는 모든 정책들 중에 얻게 되는 가장 좋은 정책을 따를 때의 가치를 나타내는 함수이다.
\(q_{*}(s, a) = \underset{\pi}{\mathrm{max}} \; q_{\pi}(s, a)\)
\(q_[*]\)를 알게 되는 순간 우리는 주어진 MDP에서 순간마다 최적의 행동을 선택하며 움직일 수 있다.
상태마다 \(q_{*}\)의 값이 가장 높은 액션을 선택하면 되기 때문이다.
\(\pi_{*} = \underset{a}{\mathrm{argmax}} \; q_{*}(s, a)\)
그러나 우리의 목적은 최적의 액션-가치 함수인 \(q_{*}\)를 찾는 것이다. 벨만 최적 방정식 2단계 수식을 보자.
\(q_{*}(s, a) = r_s^a+ \gamma \sum_{s' \in S} P_{ss'}^a \underset{a'}{\mathrm{max}} \; q_{*} (s', a')\)
이 수식은 MDP에 대한 정보를 현재는 모르기에 그대로 사용할 수 없다.
이런 상황에서는 기댓값을 사용하여 기댓값 부분을 여러 개의 샘플을 이용해 계산하고 여러 번 경험을 쌓은 다음 평균을 내었다. 이번에도 마찬가지로 벨만 최적방정식 0단계 수식을 이용해보자.
\(q_{*}(s, a) = \mathbb{E}_{s'} [r + \gamma \; \underset{a'}{\mathrm{max}} \; q_{*} (s', a')]\)
마찬가지로 기댓값 안의 부분을 여러 샘플을 통해 계산해주면 된다.
위 식을 이용해 TD학습을 하면 된다.
SARSA와 비교해보자
SARSA : \(Q(S, A) \gets Q(S, A) + \alpha (R + \gamma Q(S', A') - Q(S, A))\)
Q러닝 : \(Q(S, A) \gets Q(S, A) + \alpha (R + \gamma \; \underset{A'}{\mathrm{max}} \; Q(S', A') - Q(S, A))\)
Q러닝 식에서
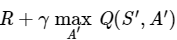
이 TD 타깃 부분은 벨만 최적 방정식의 기댓값 안의 항을 그대로 옮겨 적은 것임을 알 수 있다.
이렇게 비슷한데 SARSA는 on-policy이고, Q러닝은 off-policy인 이유는 무엇일까?
| SARSA | Q러닝 | |
| 행동 정책 | Q에 대해 ε-greedy |
Q에 대해 ε-greedy |
| 타깃 정책 | Q에 대해 ε-greedy |
Q에 대해 greedy |
행동 정책에는 탐험을 위한 ε값이 들어가 있는 반면 타깃 정책은 순수하게 Q값이 가장 높은 액션을 선택하는 방식인 greedy방식을 따르고 있다. 행동 정책과 타깃 정책이 다른 것이다.
SARSA는 벨만 기대 방정식이 뼈대였고 Q러닝은 벨만 최적 방정식에 그 기원을 두고 있다.
SARSA : \(q_{\pi}(s_t, a_t) = \mathbb{E}_{\pi} [r_{t+1} + \gamma q_{\pi}(s_{t+1}, a_{t+1})]\)
Q러닝 : \(q_{*}(s_t, a_t) = \mathbb{E}_{s'} [r + \gamma \; \; \underset{a'}{\mathrm{max}} \; q_{*}(s', a')]\)
둘다 기댓값 연산자이지만 \(E_\pi\)는 정책 함수 \(\pi\)를 따라가는 경로에 대해서 기댓값을 취하라는 의미이다. 우리는 샘플 기반 방법론을 통해 \(\pi\)가 주어진 환경 위에서 동작한 여러 개의 샘플을 통해 평균을 내는 식으로 위 기댓값을 구했다. 주어진 환경 위에서 \(\pi\)가 움직이면 자연스레 \(\pi\)(a|s)와 \(p_{ss'}^a\)가 고려되어 샘플을 얻기에 안전한 방법이다.
그러나 \(E_{s'}\)은 정책과는 관련이 없다. \(p_{ss'}^a\)만 있을 뿐 \(\pi\)와 관계된 항이 없다. 이는 \(E_{s'}\)를 계산할 때에 어떠한 정책을 사용해도 상관없다는 것을 의미한다.
그러니 임의의 정책을 사용해 데이터를 모으면 그 데이터 안에 \(p_{ss'}^a\)가 모두 반영되어 샘플이 모이고, 샘플을 이용해 기댓값을 계산할 수 있다.
왜 \(\pi\)가 없어졌을까? 이는 해당 식이 벨만 최적 방정식이기 때문이다. 벨만 최적 방정식은 모든 정책 중 최적의 정책에 대한 식이다. 최적 정책은 환경에 의존적이다. 따라서 환경을 잘 탐험하면 최적 정책을 찾을 수 있으며 여기서 환경을 탐험하는데 사용하는 정책은 어떤 정책이든 상관 없는 것이다.
Q러닝 구현
# QAgent 클래스
class QAgent():
def __init__(self):
self.q_table = np.zeros((5,7,4)) # 마찬가지로 Q테이블을 모두 0으로 초기화
self.eps = 0.9 # 입실론 설정
def select_action(self, s):
x, y = s
coin = random.random()
if coin < self.eps:
action = random.randint(0,3)
else:
action_val = self.q_table[x,y,:]
action = np.argmax(action_val)
return action
def update_table(self, transition):
s, a, r, s_prime = transition
x, y = s
next_x, next_y = s_prime
# Q러닝 업데이트 식을 이용
self.q_table[x,y,a] =self.q_table[x,y,a]+0.1*(r + np.argmax(self.q_table[next_x,next_y,:]) - self.q_table[x,y,a])
def anneal_eps(self):
self.eps -= 0.01
self.eps = max(self.eps, 0.2)
def show_table(self):
q_lst = self.q_table.tolist()
data = np.zeros((5,7))
for row_idx in range(len(q_lst)):
row = q_lst[row_idx]
for col_idx in range(len(row)):
col = row[col_idx]
action = np.argmax(col)
data[row_idx, col_idx] = action
print(data)
마무리
이번 챕터에서는 MDP의 정보를 모를 때의 상황에서 컨트롤 방법을 다뤄보았다. MDP의 전이 확률이나 보상 함수를 알지 못하기에 챕터 4의 정책 이터레이션을 그대로 사용할 수 없었다. 그래서 정책 평가 단계에 챕터 5에서 배운 모델-프리 가치 평가 방법론을 끼워 넣고 v(s) 대신 q(s,a)를 학습하는 방식으로 정책 이터레이션을 수정하였다.
'바닥부터 배우는 강화 학습' 카테고리의 다른 글
| [ 바닥부터 배우는 강화 학습 ] 08. 가치 기반 에이전트 (1) | 2024.01.08 |
|---|---|
| [ 바닥부터 배우는 강화 학습 ] 05. MDP를 모를 때 밸류 평가하기 (3) | 2024.01.02 |
| [ 바닥부터 배우는 강화 학습 ] 04. MDP를 알 때의 플래닝 (0) | 2023.11.10 |
| [ 바닥부터 배우는 강화 학습 ] 03. 벨만 방정식 (1) | 2023.10.04 |
| [ 바닥부터 배우는 강화 학습 ] 02. 마르코프 결정 프로세스 (0) | 2023.09.28 |
